EXPERIENCIA DE APRENDIZAJE 9:
"Nuestro Bicentenario nos desafía a promover acciones responsables para valorar y conservar nuestro patrimonio natural"
SITUACIÓN SIGNIFICATIVA INTEGRADA:
Este año conmemoramos el bicentenario de la independencia del Perú. Nuestro país se caracteriza por poseer una gran riqueza natural. Sin embargo, debemos preguntarnos si estamos valorando el patrimonio natural de nuestra localidad y el país, como, por ejemplo, nuestra Amazonía, que constituye uno de los pulmones más grandes del planeta y alberga ecorregiones importantes. Debemos tener en cuenta, asimismo, que el suelo de estos espacios naturales está siendo contaminado y deteriorado por actividades como la minería ilegal y la tala de árboles. Ante ello, surge la siguiente pregunta: ¿Qué compromisos y acciones asumirías para valorar y conservar el patrimonio natural de tu comunidad?
- Reconoce los elementos, propiedades y ángulos de una circunferencia.
- Usa procedimientos de cálculo para determinar ángulos de la circunferencia.
- Combina y adapta estrategias, recursos, métodos gráficos, procedimientos y propiedades algebraicas para solucionar problemas con ángulos en la circunferencia de la naturaleza.
Propósito:
Reconocer los elementos y propiedades de los ángulos de una circunferencia aplicados a la naturaleza.
SITUACIÓN SIGNIFICATIVA:
¿Qué elementos tiene la circunferencia?
¿Cuáles son los ángulos de la circunferencia que se visualizan en la figura?
RECORDEMOS:
- Centro: Punto central. Está a la misma distancia del resto de puntos de la circunferencia.
- Radio: Segmento que une el centro con un punto cualquiera de la circunferencia.
- Diámetro: Segmento que une dos puntos de la circunferencia pasando por el centro. Mide el doble que el radio.
- Cuerda: Une dos puntos de la circunferencia sin pasar por el centro.
- Arco: Porción de circunferencia limitada por una cuerda.
- Semicircunferencia: Es la mitad de una circunferencia.
Posiciones de una recta respecto de una circunferencia
- Recta tangente: Recta que tiene un punto en común con la circunferencia.
- Recta secante: Recta que tiene dos puntos en común con la circunferencia.
- Recta exterior: Recta que no tiene ningún punto en común con la circunferencia.
1.2. ELEMENTOS DEL CÍRCULO
- Semicírculo: Mitad de un círculo. El diámetro divide al círculo en dos semicírculos.
- Sector circular: Porción de círculo limitada por dos radios y su arco.
- Segmento circular: Porción de círculo limitada por una cuerda y su arco.
- Corona circular: es la porción de círculo limitada por dos círculos concéntricos.
- Trapecio circular: es la porción de la corona circular, limitado por dos radios.
donde r es el radio, d el diámetro y π ≈ 3.141592654 .
1. Ángulo Central
El ángulo central, cuyo vértice se encuentra en el centro de la circunferencia «O», sus lados son dos radios.

«La medida del ángulo central es igual a la medida del arco comprendido entre sus lados».
2. Ángulo Inscrito
En este caso el vértice se encuentra sobre la circunferencia, el punto «B» y sus lados son dos cuerdas.

«La medida del ángulo inscrito es igual a la mitad de la medida del arco comprendido entre sus lados».
3. Ángulo Semi-Inscrito
En este ángulo, el vértice se encuentra sobre la circunferencia, sus lados son una tangente y una cuerda.

«La medida del ángulo semi-inscrito es igual a la mitad del arco correspondiente a la cuerda».
4. Ángulo Ex-Inscrito
El vértice de este tipo de ángulo se encuentra sobre la circunferencia.

«El ángulo ex-inscrito es el ángulo adyacente y suplementario del ángulo inscrito».
5. Ángulo Exterior
El vértice del ángulo exterior se encuentra en la zona exterior a la circunferencia, sus lados pueden ser dos segmentos secantes, dos tangentes o una secante y una tangente.
«La medida del ángulo exterior es igual a la semidiferencia de los arcos formados por los lados».
Véase las siguientes figuras:
Caso I: Ángulo entre Dos Secantes:

Caso II: Ángulo entre Dos Tangentes:

Caso III: Ángulo entre una Recta Tangente y otra Secante:

6. Ángulo interior
El vértice del ángulo interior se encuentra en un punto de la circunferencia, sus lados pueden ser dos cuerdas, que se cruzan.
Propiedades Fundamentales en la Circunferencia
1.- Si AB es diámetro:

2.- Si T es punto de Tangencia:

3.- Si PA y PB son tangentes:

4.- Si AB ⊥ OM

5.- Si AB=CD:

6.- Si AB // CD:

7.- Si A y B son puntos de tangencia:

8.- Si A, B y C son puntos de tangencia:

9.- Si A, B y C son puntos de tangencia:

10.- AB y CD : Tangentes Exteriores
MN y PQ : Tangentes Interiores











Teorema de Pithot
En todo cuadrilátero circunscrito a una circunferencia se cumple que la suma de las longitudes de dos lados opuestos es igual a la suma de las longitudes de los otros dos lados.


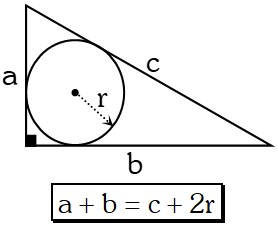
Teorema de Poncelet
En todo triángulo rectángulo se cumple que la suma de las longitudes de sus catetos es igual a la suma de la longitud de su hipotenusa y la longitud del diámetro de la circunferencia inscrita en dicho triángulo.

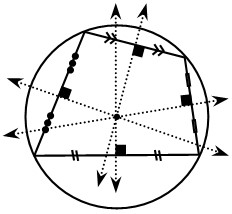
Cuadrilátero Inscriptible
Llamado también cuadrilátero cíclico. Un cuadrilátero es inscriptible si por los cuatro vértices puede pasar una circunferencia. Las mediatrices de los lados de este cuadrilátero se intersecan en un punto, que puede estar situado en el interior o en el exterior, constituyéndose en el centro de la circunferencia circunscrita.
Por lo general se estudia dos condiciones de inscriptibilidad, que permitan asegurar la existencia de la circunferencia circunscriptible al cuadrilátero.

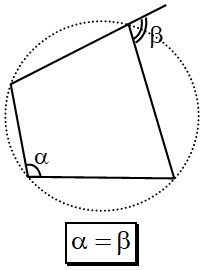
Primera Condición:
Un cuadrilátero es inscriptible si los ángulos opuestos son suplementarios. Es decir:

Esta condición es equivalente a decir que un ángulo interior del cuadrilátero es congruente al ángulo opuesto exterior.


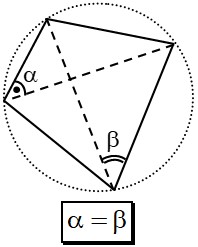
Segunda Condición:
Un cuadrilátero es inscriptible si el ángulo formado por un lado y una diagonal es congruente al ángulo formado por el lado opuesto y la otra diagonal.

Observaciones:
– Los cuadriláteros que SIEMPRE son inscriptibles son el cuadrado, el rectángulo y el trapecio isósceles.
– El trapecio rectángulo, el trapecio escaleno, el rombo y el paralelogramo no son inscriptibles.
– Si en un triángulo se unen los pies de dos alturas se forma un cuadrilátero inscriptible.
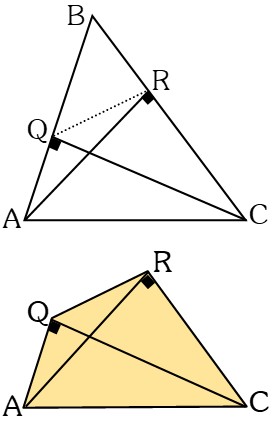
Nota: Nótese que los triángulos ABC y BQR son semejantes entre sí.
– El trapecio rectángulo, el trapecio escaleno, el rombo y el paralelogramo no son inscriptibles.
– Si en un triángulo se unen los pies de dos alturas se forma un cuadrilátero inscriptible.

Problemas Resueltos
Problema 01:
Calcular x en la siguiente figura. Si «A» y «B» son puntos de tangencia.

Resolución:
En este ejercicio aplicaremos las fórmulas del ángulo inscrito y exterior de la circunferencia, veamos:

– Por ángulo inscrito: Arco AB = 2(60°) = 120°
– Por ángulo exterior en APC: x + 120° = 180°
∴ x = 60°
Problema 02:
Hallar «x», si «O» es centro de la circunferencia.

Resolución:
Trazamos el radio OB para formar el ángulo central en la circunferencia y a la vez el triángulo AOB.

- Por ángulo central: m∡AOB = arco AB = 140°.
- El triángulo AOB es triángulo isósceles, entonces trasladamos el ángulo «x».
Por último, aplicamos propiedad de triángulos en el Δ AOB: «suma de ángulo internos»
⇒ x + x + 140 = 180°
∴ x = 20°
Problema 03:
En la circunferencia, A y B son puntos de tangencia, calcule «x»

Resolución:
En este problema aplicaremos la propiedad del ángulo inscrito:
Arco AB = 2(∠ACB) = 2x

Siendo A y B puntos de tangencia y P un punto exterior, se cumple la siguiente propiedad:

En el problema:
2x + 90° = 180
⇒ x = 45°
∴ x = 45°
Problema 04:
Si el arco BC mide 72° y «O» es centro de la circunferencia. Calcular: θ

Resolución:
En la figura: el ∠BOC es el ángulo central, entonces:
∠BOC = 72°
También, por ángulo inscrito:
∠BAC = 36°

Propiedad en el cuadrilátero ABOC:
36° + θ + 2θ = 72°
⇒ θ = 12°
∴ θ = 12°
Problema 05:
En la figura AC es diagonal de la circunferencia y m∠ABT = 36°. Hallar el ángulo «x»

Resolución:
Al ser «O» centro de la circunferencia, se traza OT para aprovechar el ángulo de tangencia (90°).
En «T» vemos el ángulo semi-inscrito:
⇒ Arco AT= 2(x) = 2x

Por ángulo central:
∠AOT = Arco AT= 2x
En «O»:
2x + 54° = 180° (ángulo llano)
Resolviendo:
∴ x = 63°
Problema 06:
En la figura se cumple: x+y=125°. Calcular la medida del arco BD de la circunferencia.

Resolución:
Nos piden el arco BD =??
Vea que los ángulos «x» e «y» son ángulos interiores y exteriores respectivamente de la circunferencia. Veamos cada propiedad:
Por ángulo externo:
x = (arco BD – arco AC)/2 …..(1)
Por ángulo interno:
y = (arco BD + arco AC)/2 …..(2)
Sumando las expresiones (1) y (2):
x + y = arco BD
Por dato: x + y = 125°
∴ Arco BD = 125°








Comentarios
Publicar un comentario