SESIÓN 19: REPRESENTAMOS UNA FUNCIÓN CUADRÁTICA AL RESOLVER SITUACIONES SIGNIFICATIVAS

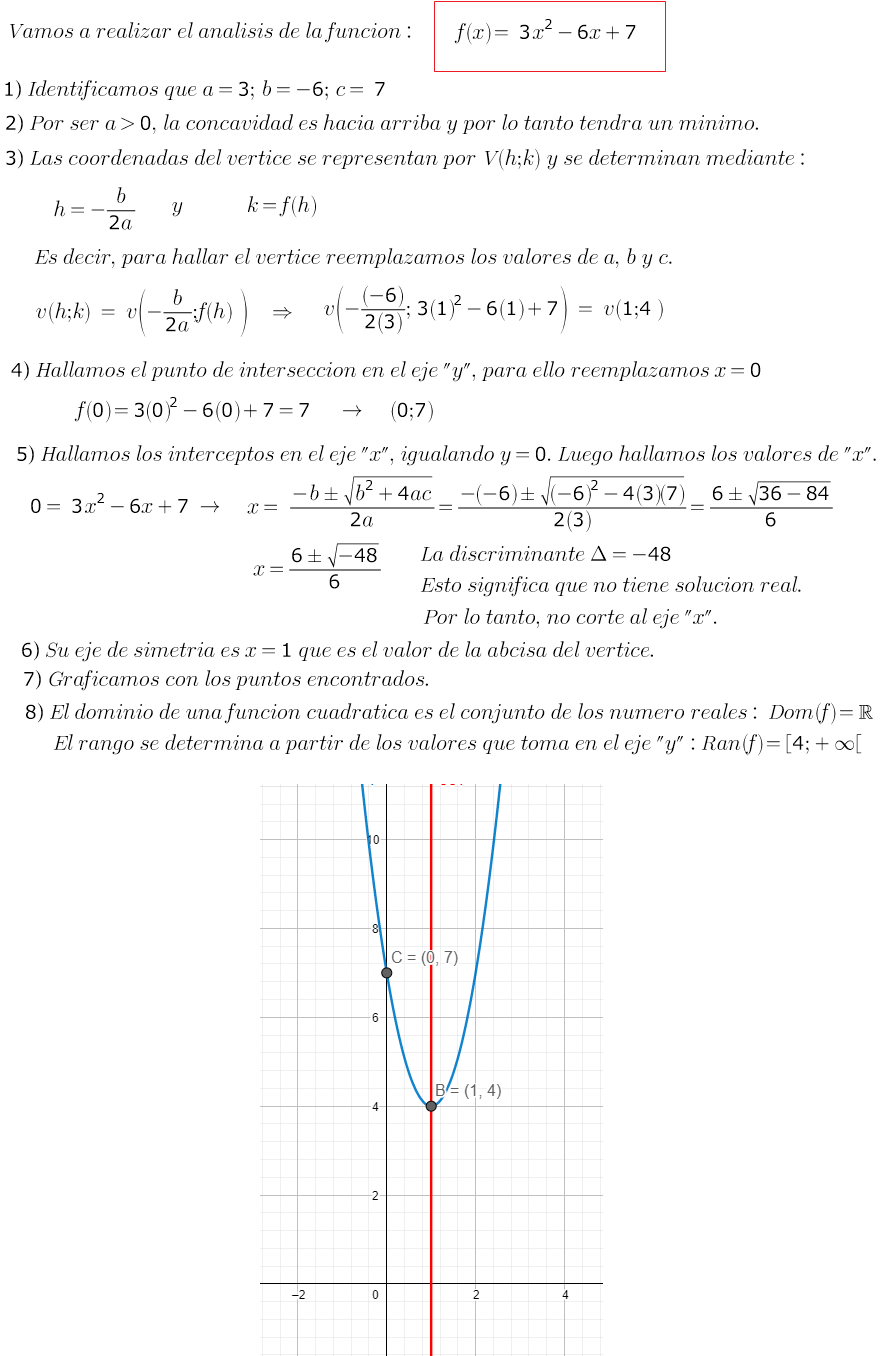
EXPERIENCIA DE APRENDIZAJE 6:

" Conservamos nuestra salud y el ambiente con responsabilidad"

SITUACIÓN SIGNIFICATIVA INTEGRADA:

La pandemia ha ocasionado un mayor sedentarismo en la comunidad Soranina y también disminución de la actividad física. Esto nos expone a problemas de salud como el sobrepeso y la obesidad, la hipertensión o los males cardiovasculares, que constituyen factores de riesgo para desarrollar casos graves de COVID-19. Al respecto, la Organización Mundial de la Salud (OMS) recomienda que todas las personas deben realizar actividades físicas. Además, señala que un gran número de muertes podrían evitarse si la población fuera más activa. Por ello, es importante que evaluemos, nuestro rol en la protección y promoción de la salud y el ambiente. Ante esta situación, te proponemos responder a la pregunta y cumplir el reto: ¿Nuestras acciones sobre el cuidado de la salud están en armonía con la naturaleza? ¿Qué acciones podemos realizar para cuidar nuestra salud y el ambiente?

Criterios de evaluación:

• Establece relaciones entre datos de variación de cantidades y las transforma a funciones cuadráticas.
• Evalúa si la función cuadrática que planteó representa las condiciones del problema de determinar el área máxima.
• Expresa con representaciones tabulares, gráficas y lenguaje algebraico su comprensión de la gráfica de una función (sus valores máximos y mínimos, sus interceptos, su eje de simetría, su vértice y su orientación).
• Selecciona y combina estrategias, métodos, recursos y procedimientos más convenientes para representar funciones cuadráticas según las condiciones del problema.

Propósito:

En esta actividad, utilizaremos la función cuadrática para determinar el área máxima en el que podemos realizar nuestras actividades físicas. A partir de ello, plantearemos conclusiones sobre la utilidad de la función cuadrática para determinar los espacios en los que podemos realizar actividades físicas en beneficio de nuestra vida saludable, para luego considerarlas en nuestro plan integral.

SITUACIÓN SIGNIFICATIVA:

Nuestros niveles de oxígeno en la sangre jamás habían resultado tan importantes como hasta ahora. Ahora que somos más conscientes de su importancia, ¿Cómo podemos aumentar estos niveles de oxígeno en la sangre? Los especialistas nos recomiendan realizar ejercicios de forma regular, como los aeróbicos, correr, bailar o cardio, ya que aceleran la respiración y la hacen más profunda. Esto aumenta la cantidad de oxígeno en la sangre, lo que induce a que el corazón lata con mayor velocidad y aumente el flujo sanguíneo hacia los músculos y de regreso a los pulmones.

 

María, después de escuchar la información, decide adecuar un espacio contiguo a su casa para cuidar su salud, realizando ejercicios físicos y mejorar los niveles de oxígeno en la sangre. Ella considera que la superficie debe tener forma rectangular, la cual delimitará con 20 m de cuerda. Sabiendo que solo debe colocar la cuerda sobre tres lados, ya que el cuarto limita con su casa, ¿Cuáles serán las dimensiones de la superficie destinada para hacer ejercicios si debe tener la máxima área? ¿Cuál será el área de dicho espacio? ¿Qué tipos de ejercicios podría realizar en el espacio delimitado por la cuerda

RECORDEMOS:

FUNCIÓN CUADRÁTICA

Una función cuadrática es un tipo de función que se caracteriza por ser un polinomio de segundo grado. Una función cuadrática tiene la forma:

Donde:

a, b y c = son coeficientes y números reales y a ≠ 0. 

Además, su gráfica siempre es una PARÁBOLA, que tiene los siguientes elementos:

Dominio y rango de una función cuadrática

Otras características, con respecto al dominio y rango de la función cuadrática:

Su gráfica siempre es una parábola con vértice V(h; k). 

Su dominio es el conjunto de los números reales: Dom(f)=R

Su rango es el intervalo Ran (f)=[k; +∞[ si la parábola se abre hacia arriba, 

y Ran=]−∞; k], si la parábola se abre hacia abajo. 

El punto donde la función alcanza su valor máximo o mínimo, es el vértice. Las funciones cuadráticas son continuas porque no presentan corte en su brazo y tienen un eje de simetría.

La localización del vértice de una parábola es muy importante en la resolución de problemas relacionados con maximizaciones o minimizaciones de ganancias, costos, dimensiones, etc. 

GRÁFICA DE UNA FUNCIÓN CUADRÁTICA

En una función cuadrática, la gráfica depende del valor de "a", así: 

• El signo de a indica la concavidad de la parábola. Si es positivo, la concavidad es hacia arriba, y si es negativo, la concavidad es hacia abajo. 

• El valor absoluto de a modifica la abertura de las parábolas; cuanto menor es el valor de |a|, la parábola es más abierta, y cuando mayor es |a|, la parábola es más cerrada.

PASOS RECOMENDADOS PARA GRAFICAR UNA FUNCIÓN:

Para construir una gráfica de parábola se requiere conocer los siguientes elementos:

 

a) Vértice

Encontrar las coordenadas del vértice en términos de los coeficientes de la forma general: 

Las coordenadas de "x" se calcula mediante la expresión: 

Conociendo la coordenada de "x", podemos determinar el valor "y", mediante:

Las coordenadas del vértice sería: v(h; k)

b) Sentido de la parábola

• Si a > 0 (positivo), entonces la parábola abre hacia arriba.
• Si a < 0 (negativo), entonces la parábola abre hacia abajo.

c) Ecuación del eje de simetría

Así mismo, la ecuación del eje de simetría es:  x= h

d) Puntos de corte con los ejes coordenados:

• Con el eje Y

Para encontrar la intersección con el eje "Y", igualar x = 0  , por lo que tendremos:

(0;c) es el punto donde la parábola corta al eje "y"

• Con el eje X

Para encontrar el valor de "x", igualamos y = 0, por lo que tendremos que resolver la siguiente igualdad:

  

Para hallar los valores de "x" o raíces de la parábola, puedes usar factorización o fórmula general:

Al resolver la ecuación anterior los resultados pueden ser:

1.    Dos puntos de corte:  (x1; 0) y (x2; 0),  esto sucede si:  
2.    Un punto de corte: (x1; 0),  esto sucede si:   

3.    Ningún punto de corte si:      

 e) Graficamos

Representar los puntos y trazar la parábola de acuerdo con las informaciones recabadas. Graficamos los cortes obtenidos y con las informaciones anteriores, podemos realizar un bosquejo de la parábola, intentando que sea simétrica en torno a la recta vertical o eje de simetría que pasa por el vértice. 

Video para hallar el vértice y graficar tabulando:

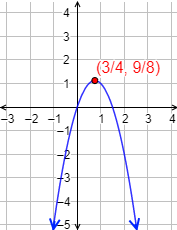
Ejemplo para hallar el vértice:

Calculamos el vértice de la función:

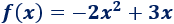
Identificamos los coeficientes:

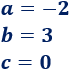
Como $a$ es negativo, la parábola tiene forma de $\cap$. El vértice es un máximo.

La primera coordenada "h" del vértice se determina con la siguiente fórmula: 

h = - b/2a 

h= -(3)/2(-2) = 3/4

Calculamos la segunda coordenada "k" del vértice, se determina reemplazando en la función f(x) el valor de "h":

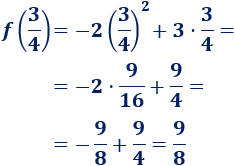
Por tanto, el vértice (h;k) es el punto:

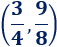
Gráfica:

Ejemplos para hallar, el gráfico, eje, vértice y puntos de corte en los ejes de una función cuadrática

___________________________________________________________

ESTUDIO DE UNA FUNCIÓN CUADRÁTICA:

Recurso 1: 

Recurso 2:

Recurso 3:

Khan Academy: ¿Cómo reconocer una función cuadrática?

Practicamos en Khan Academy

Practicamos en liveworks